Engineering and Physics
Optimization in Engineering and Physics
The EDOM group has a rich history of collaborations with engineers with projects involving all kinds of engineering questions. We are specifically interested in bringing methods from discrete optimization to application in fields where they are not well established: Most engineering models are modeled with a well-established simulation model in the background. Discrete parameters are then often introduced via trial-and-error or heuristic methods. We have shown in various applications that it is possible to produce guaranteed globally optimal solutions in such cases.
In order to understand the characteristics of certain physics problems, it is helpful to study their minimum-energy states, or, if possible, the complete partition function. In this project, we focus on the area of disordered systems. Our goal is to provide effective methods and fast implementations for challenging physics problems. We focus on the design of exact solution procedures that always generate correct solutions, as this is often required by the application. A variety of our implementations is publicly available via the spin glass ground-state server.
Further details can also be found at http://cophy.informatik.uni-koeln.de/
Current Projects
Quality control by robust optimization
The long-term goal of the whole CRC1411 is the property design of single particles and particulate products made from these single particles. The objective of Subproject D06 within the CRC1411 is the development, algorithmic design, implementation and validation of robust mathematical optimization methods for protecting the design of particulate products against uncertainties. Global solution methods are investigated for optimal robust chromatography as well as synthesis processes, developing methods based on reformulation and decomposition. The obtained results are validated with the projects. Information on which uncertainties are most relevant and should be reduced, together with recommendations on robust optimum design and quality control, are returned to the experimental projects.
For more details visit: https://www.crc1411.research.fau.eu
Contact: Frauke Liers, Jana Dienstbier
Ising Spin Glasses
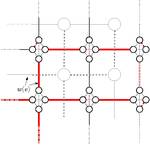
Algorithmically, minimizing the energy function for Ising spins is an unconstrained quadratic binary optimization problem that is well known to be equivalent to the max-2-cut problem. Given an edge-weighted graph, max-2-cut asks for partitioning the nodes into two disjoint sets maximizing the sum of the weights of edges connecting nodes in different partitions. Max-2-cut is in general an NP-hard problem that is also difficult in practice. For special graph classes, however, it allows solution in polynomial time. We develop exact approaches for both the NP-hard and the polynomially solvable cases of the max-2-cut problem and use them for the physics application.
Contact: Frauke Liers
Finished Projects
Potts Spin Glasses
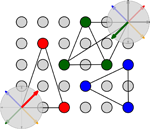
In a Potts spin glass, a spin can attain one of k states. The determination of energy-minimum states amounts to computing a maximum k-cut in the graph of interactions. Thus, the task is to partitioning the set of vertices of a graph into k disjoint subsets so as to maximize the total weight of the edges joining vertices in different partitions. We design and implement exact branch-and-cut algorithms based on semidefinite programming and cutting planes.
Another function of interest is the partition function that encodes the complete physics of a system. For Potts glasses with a large number of states, the dominant term in the partition function can be determined by solving the optimum cooperation problem that can be explained as follows. Suppose we are given a set of researchers. For each pair of researchers, we know the benefit of working together. The optimum cooperation problem asks for an assignment of people to projects such that the number of research projects covered plus the total benefit is maximum. Using graph-theoretic considerations, we considerably reduce the number of iterations of the method in practice.
Contact:Frauke Liers
Spin Glass Ground-State Server

As a service to the community, our implementations are publicly available via the spin-glass ground state server. Short- and long-range spin glass realizations of different dimensions can be submitted to the server, either through a web interface or using a command-line client. Big job batches are possible as well. Results are returned via e-mail.
Details at http://www.informatik.uni-koeln.de/spinglass/
Contact: spinglass[ät]informatik.uni-koeln.de

